替代定理(substitution theorem )
如果已知电路中第 k 条支路的电压 uk 和电流 ik ,那么无论该条支路是由何种元件构成的,它都可以用电压等于 uk 的理想电压源或电流等于 ik 的理想电流源去替代,替代之后,电路中其他支路的电压和电流均不变。

推 论:如果第 k 条支路的电压 uk 等于 0 ,那么该支路可用一条短路线去替代;如果第 k 条支路的电流 ik 等于 0 ,那么该支路可用一对断开的节点去替代。
例 4.2-1 图 4.2-2 ( a )所示电路为电桥电路,当通过电阻 Rg 的电流 Ig=0 时,电桥达到平衡。 Us=4.5V , R1=1K Ω, R2=10K Ω, R3 为可变电阻, R4 为被测电阻,现调节电阻 R3 ,当 R3=0.5K Ω时 , 电桥达到平衡。求被测电阻 R4 及电压源供出的电流 I 。

解:当电桥平衡时, ![]() ,则 Rg 电阻上的电压
,则 Rg 电阻上的电压 ![]() 。由于
。由于 ![]() ,根据替代定理, ab 支路可用一条短路线替代,如图 4.2-2 ( b )所示。显然,
,根据替代定理, ab 支路可用一条短路线替代,如图 4.2-2 ( b )所示。显然,
![]() ,
,
即
![]()
又由于 ![]() ,根据替代定理, ab 支路可用一对断开的节点替代,如图 4.2-2 ( c )所示。则
,根据替代定理, ab 支路可用一对断开的节点替代,如图 4.2-2 ( c )所示。则
![]()
![]()
上面两式相除,得
![]()
被测电阻为
![]()
再由图 4.2-2 ( b ),得电桥平衡时, c 、 d 两端的等效电阻为
Rcd= ( R1 ∥ R2 ) + ( R3 ∥ R4 ) = ( 1K ∥ 10K ) + ( 0.5K ∥ 5K ) =1.364K Ω
平衡时电压源供出的电流
![]()
注 意:替代定理对于线性电路和非线性电路都是成立的
西门子CPU模块6ES7317-2AK14-0AB0
一阶电路零输入响应的计算
计算步骤
1 、画出 ![]() 时刻的等效电路。这时电路已达到稳态,在直流激励作用时,将电容当作开路,将电感当作短路,求出
时刻的等效电路。这时电路已达到稳态,在直流激励作用时,将电容当作开路,将电感当作短路,求出 ![]() 或
或 ![]() ,并根据换路定则,求得电路的初始状态。若需要计算电路中其它响应,再根据初始状态计算这些响应的初始值。
,并根据换路定则,求得电路的初始状态。若需要计算电路中其它响应,再根据初始状态计算这些响应的初始值。
2 、求电路的时间常数τ。对于 RC 电路, ![]() ,对于 RL 电路,
,对于 RL 电路, ![]() 。其中, R 为从电容 C 或电感 L 两端看进去的戴维南等效电阻。
。其中, R 为从电容 C 或电感 L 两端看进去的戴维南等效电阻。
3 、求出零输入响应 ![]()
![]()
例 5.3-1 图 5.3-5 ( a )所示电路中,开关原来处于位置 1 ,且电路已处于稳态, t=0 时刻开关 S 拨到位置 2 ,求 ![]() 时的
时的 ![]() ,
, ![]() 和
和 ![]() 。
。

解: 1. 求初始值 ![]() ,
, ![]() 和
和 ![]()
作出电路换路前 ![]() 时刻的等效电路,如图 5.3-5 ( b )所示,这时电路处于稳态,电容相当于开路,并由换路定则得
时刻的等效电路,如图 5.3-5 ( b )所示,这时电路处于稳态,电容相当于开路,并由换路定则得
![]()
![]() 时刻的等效电路如图 5.3-5 ( c )所示,两个 100 K Ω的电阻并联,
时刻的等效电路如图 5.3-5 ( c )所示,两个 100 K Ω的电阻并联,
![]()
![]()

2 .求时间常数τ
图 5.3-5 ( c )电路中无外加激励,只有电容的初始电压通过两个电阻放电,产生的响应为零输入响应。这时,从电容两端看进去的戴维南等效电阻是两个 100 K Ω的电阻并联,R=100K ∥ 100K=50K Ω
则时间常数为![]()
3 .电路换路后 ![]() 时的响应为
时的响应为
![]()
![]()
![]()
![]()
![]()
![]()
一、网孔电流方程
出发点
减少方程数,用未知的网孔电流代替未知的支路电流来建立方程。
图3.3-1所示电路,共有n=4个节点,b=6条支路(把电压源和电阻串联的电路看成一条支路)。显然,独立的网孔数为b-n+1=3个。

1、网孔电流
设想每个网孔中有一个假想的电流沿着构成该网孔的各条支路循环流动,把这一假想的电流称为网孔电流(mesh current),如图3.3-1中的![]() 分别表示网孔a、b、c的网孔电流。电路中各支路电流就可以用网孔电流表示
分别表示网孔a、b、c的网孔电流。电路中各支路电流就可以用网孔电流表示

结 论:用3个网孔电流表示了6个支路电流。减少了方程数。
2、网孔电流方程
根据KVL,可得图3.3-1电路的网孔电流方程

网孔电流方程的一般形式
自电阻×本网孔电流±Σ(互电阻×相邻网孔电流)= 本网孔中沿网孔电流方向的所有电压源的电位升之和
自电阻(self resistance)是各网孔中所有支路电阻之和,互电阻(mutual resistance)是两个相邻网孔之间的共有电阻。第二项前的正负号由相邻网孔电流与本网孔电流在互电阻上流过的方向是否一致来决定,若一致取正号;取负号。
网孔电流法分析电路的一般步骤
确定电路中的网孔数,并设定各网孔电流的符号及方向。按常规,网孔电流都取顺时针或逆时针方向。列写网孔电流方程,并求解方程,求得各网孔电流。由求得的网孔电流,再求其他的电路变量,如支路电流、电压等。
例3.3-1 图3.3-1所示电路中,已知us1=21V,us2=14V,us3=6V,us4=us5=2V,R1=3Ω,R2=2Ω,R3=3Ω,R4=1Ω,R5=6Ω,R6=2Ω,求各支路电流。
解:1. 电路的网孔为3个。设定3个网孔电流的符号及方向如图3.3-1所示。
2.列写网孔方程
网孔a: ![]()
网孔b: ![]()
网孔c: ![]()
代入参数,并整理,得
解得网孔电流为: ![]()
3.由网孔电流求各支路电流![]()
![]()
![]()
![]()
2、全欧姆定律
只有一个网孔的电路,称为单回路电路(single loop circuit)。对于单回路电路,有全欧姆定律。
全欧姆定律:对于单回路电路,回路电流i等于沿回路电流方向的所有电压源的电压升的代数和除以回路中所有电阻之和。![]()
二、含有电流源的电路
1、有伴电流源
结 论:如果电路中的电流源是有伴电流源,将有伴电流源等效成有伴电压源。
方法一 把电流源当电压源处理
设定电流源两端的电压,列写网孔方程,利用电流源的电流与网孔电流之间的关系再补充一个方程。
2、无伴电流源
电流源处于边界支路上
结 论:电流源所在网孔的网孔电流即为电流源的电流,可以少列一个网孔方程。
例3.3-2 图3.3-2所示电路中,试用网孔电流法求流过3Ω电阻的电流I1。

解:电路中含有一个2A电流源,处于网孔a的边界支路上。取顺时针方向为各网孔电流的方向,则![]() (1)
(1)
只需列写两个网孔方程,
网孔b: ![]() (2)
(2)
网孔c: ![]() (3)
(3)
经整理后,得![]()
解得网孔电流为: ![]()
流过3Ω电阻的电流为![]()
2)电流源处于相邻网孔的公共支路上

例3.3-3 电路如图3.3-3所示,试用网孔电流法求各网孔电流。
解:电路中的1A电流源处于网孔a、b的公共支路上。设它的两端电压为U,并将它当作电压源看待,列写网孔方程,
网孔a: ![]() (1)
(1)
网孔b: ![]() (2)
(2)
网孔c: ![]() (3)
(3)
补充方程: ![]() (4)
(4)
整理后得
解上述方程组,得网孔电流为![]()
方法二 超网孔(super mesh)方法
把以电流源为公共支路的两个网孔当作一个超网孔处理,使电流源所在支路不出现在超网孔的支路中。
注 意:列写超网孔方程时,由于电流源与1Ω电阻串联的支路没有出现在超网孔中,这条电流源支路不应计算进去。
利用超网孔的方法计算例3.3-3。
对超网孔: ![]() (1)
(1)
对网孔c: ![]() (2)
(2)
补充方程: ![]() (3)
(3)
整理后得,
解方程组,得网孔电流为![]()
三、含有受控源电路
思 路:把受控源当独立源看待。当然,如果受控源的控制量不是网孔电流,应再补充一个能反映控制量与某网孔电流之间关系的方程式。
例3.3-4 电路如图3.3-4所示,试网孔电流法求受控源发出的功率。

解:电路中有一个受控电流源,是无伴电流源,设其两端电压为U1,把它当独立的电压源看待。
设3个网孔的网孔电流分别为![]() ,其方向均为顺时针方向,如图3.3-5所示,列写网孔方程,
,其方向均为顺时针方向,如图3.3-5所示,列写网孔方程,
网孔a: ![]() (1)
(1)
网孔b: ![]() (2)
(2)
网孔c: ![]() (3)
(3)
补充方程: ![]() (4)
(4)![]() (5)
(5)
以上5个方程联立求解,得![]()
![]()
受控源的电流为 ![]()
受控源发出功率为![]()
现场调试的时候,已经写好的程序(未调试过),下载进plc中后 发现报错,无法启动之类的问题
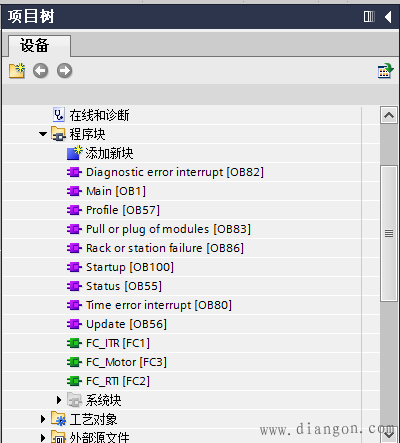
在程序中需要添加加入 0B55 OB56 OB57 OB82 OB83 OB100
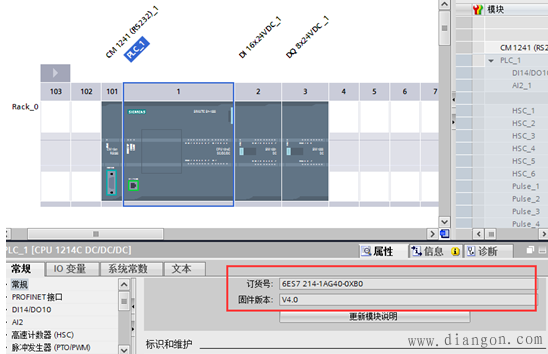
解决方法: 查看硬件组态是否出错
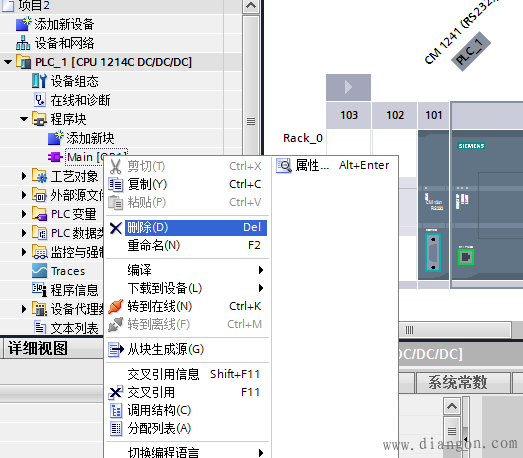
如果硬件组态无错 将原来的程序(带硬件组态)另保存一下 将其中的原来的程序块删除,只保留硬件组态,并下载如PLC中
断电在上电 如果正常再将原来的程序下载(一般都能成功启动) 如果不正常则是PLC外部接线或者PLC硬件的错误,与程序无关
|