西门子6ES7217-1AG40-0XB0技术参数

1.步距误差

是指空载时实测的步距角与理论的步距角之差。它反映了步进角位移的精度。

国产步进电动机的步距误差一般在±10′～±30′范围内，精度较高的步进电动机可达±2′～±5′。

2.大静转矩

是指步进电动机在某相始终通电而处于静止不动状态时，所能承受的大外加转矩，亦即所能输出的大电磁转矩。它反映了步进电动机的制动能力和低速步进运行时的负载能力。

3.启动矩频特性

是指步进电动机在有外加负载转矩时，不失步地正常启动所能接受的大阶跃输入脉冲频率(又称启动频率)与负载转矩的对应关系。

90bf002型步进电动机的启动矩频特性曲线

4.启动惯频特性

是指步进电动机带动纯惯性负载启动时，启动频率与转动惯量之间的关系。

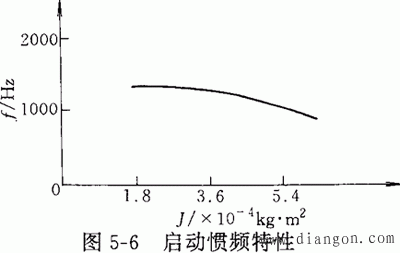
5.运行矩频特性

是指步进电动机运行时，输出转矩与输入脉冲频率的关系。***选用步进电动机时，应使实际应用的运行频率与负载转矩所对应的运行工作点位于运行矩频特性之下，才能保证步进电动机不失步地正常运行。***

6.步进运行和低频振荡

当输入脉冲频率很低时，脉冲周期如大于步进电动机的过渡过程时间，步进电动机就会处于一步一停的运行状态，这种运行状态称为步进运行。步进电动机都有一较低的固有频率，当步进运行频率或低速运行频率与该固有频率相等或接近时，就会产生共振，使步进电动机振荡不前，这种现象称为低频振荡。

避免低频振荡的现象发生采用的方法：

一种是使运行频率避开固有频率，二是前一方法不允许时，可通过调节步进电动机上的阻尼器来改变固有频率。

7.大相电压和大相电流

分别是指步进电动机每相绕组所允许施加的大电压和流过的大电流。

一、伺服负载转矩的计算

二、电动机大转矩的确定

伺服电动机在快速启动时的负载转矩一般比正常运行时的负载转矩要大得多，所以电动机的大转矩常按启动时的负载转矩来确定，即要求：

tq—电动机启动时的负载转矩；

tmax—电动机的大转矩；

tr—电动机的额定转矩；

λ—电动机的瞬时过载系数。

三、电动机额定转矩的确定

伺服电动机额定转矩tr可按连续运行时作用在电动机轴上的负载转矩t来确定，即要求

当系统精度要求较高或负载较大时，开环伺服系统往往满足不了要求，这时应采用闭环或半闭环控制的伺服系统。

从控制原理上讲，闭环控制与半闭环控制是一样的，都要对系统输出进行实时检测和反馈，并根据偏差对系统实施控制。

两者的区别仅在于检测信号位置的不同，因而导致设计、制造的难易程度不同及工作性能的不同，但两者的设计与分析方法是基本上一致的。

一、系统方案设计

(一)闭环或半闭环控制方案的确定

当系统精度要求很高时，应采用闭环控制方案。

闭环伺服系统结构复杂，设计难度大，成本高，尤其是机械系统的动态性能难于提高，系统稳定性难于保证。因而除非精度要求很高时，一般应采用半闭环控制方案。目前大多数和工业机器人中的伺服系统都采用半闭环控制。

(二)执行元件的选择

直流伺服、交流伺服电动机或伺服阀控制的液压伺服马达作为执行元件。

(三)检测反馈元件的选择

常用的位置检测传感器有旋转变压器、感应同步器、码盘、光电脉冲编码器、光栅尺、磁尺等。

①被测量为直线位移，应选尺状的直线位移传感器，如光栅尺、磁尺、直线感应同步器等。

②被测量为角位移，应选圆形的角位移传感器，如光电脉冲编码器、圆感应同步器、旋转变压器、码盘等。

在位置伺服系统中，为了获得良好的性能，往往还要对执行元件的速度进行反馈控制，因而还要选用速度传感器。交、直流伺服电动机常用的速度传感器为测速发电机。目前在半闭环伺服系统中，也常采用光电脉冲编码器，既测量电动机的角位移，又通过计时而获得速度。

(四)机械系统与控制系统方案的确定

机械传动与执行机构在结构形式上与开环控制的伺服系统基本一样，即由执行元件通过减速器和滚动丝杠螺母机构，驱动工作台运动。

控制系统方案的确定：

主要包括执行元件控制方式的确定和系统伺服控制方式的确定。

对于直流伺服电动机，应确定是采用晶体管脉宽调制(pwm)控制，还是采用晶闸管(可控硅)放大器驱动控制。对于交流伺服电动机，应确定是采用矢量控制，还是采用幅值、相位或幅相控制。

伺服系统的控制方式有模拟控制和数字控制，每种控制方式又有多种不同的控制算法。

还应确定是采用软件伺服控制，还是采用硬件伺服控制，以便据此选择相应的计算机。

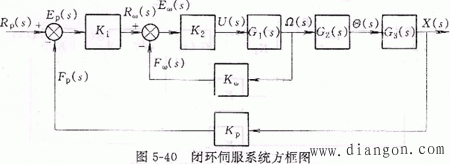
二、系统性能分析

(一)系统的数学模型

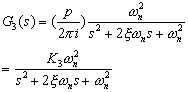
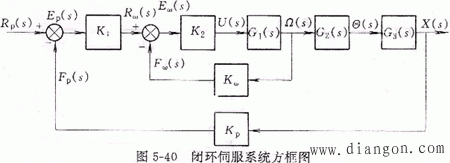
(二)数学模型的简化

1.简化成一阶系统

假如系统中各环节都是理想的，没有惯性，没有阻尼，刚性为无穷大。

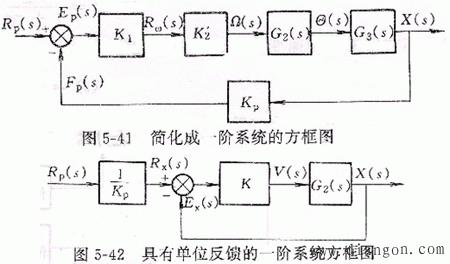
k值大的伺服系统称为硬伺服或高增益系统，k值小的称为软伺服或低增益系统。

2.简化成二阶系统

当机械系统的刚度非常大，惯性非常小，其固有频率远远大于伺服电动机固有频率时，伺服系统的动态特性就主要取决于伺服电动机速度环的动态特性。

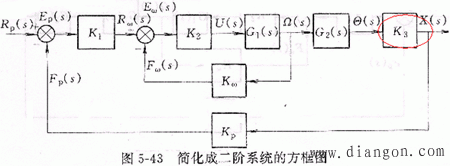
采用大惯量直流伺服电动机的中小型伺服系统和半闭环控制的伺服系统大多数都属于这种情况。

3.简化成三阶系统

当机械系统固有频率远低于伺服电动机固有频率时，伺服系统的动态特性主要取决于机械系统，则系统可简化成三阶系统。

属于这种情况的有：

小惯量直流伺服电动机的中小型伺服系统或大惯量直流伺服电动机的大型伺服系统

(三)系统稳定性及快速响应性分析

利用数学模型对系统性能进行分析，找出系统各参数对系统性能的影响关系，以便在设计时合理选择各参数。

1.一阶系统分析

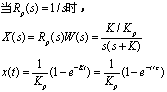
如取位置传感器的比例系数kp＝1

2.二阶系统分析

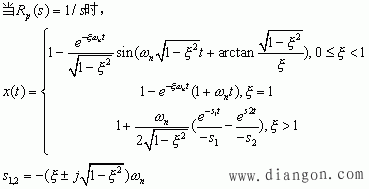
3.三阶系统分析

比例、积分环节的对数幅频及相频特性表达式为：

振荡环节的对数幅频及相频特性表达式为：

(四)系统精度分析

系统在稳定状态下，其输出位移与输入指令信号之间的稳态误差δ为：

式中：

δ1—与系统的构成环节及输入信号形式有关的误差，称为跟踪误差；

δ2—由负载扰动所引起的稳态误差。

1.跟踪误差

位置伺服系统属于i型系统。

系统在跟踪阶跃输入时的跟踪误差δ1＝0mm；

在跟踪等速斜坡输入时，其跟踪误差为

式中：

v—输入的速度指令(mm/s)；

k—系统的开环增益(s-1)。

2.负载扰动所引起的误差

对于i型系统，由负载扰动所引起的稳态误差δ2(mm)可用下式计算

式中：

k3－机械系统的转换系数(mm/rad)， k3＝p/(2πi) ；

tl－折算到电动机轴上的干扰转矩(n·m)；

kr－系统伺服刚度或称力增益(n·m/rad)，它定义为干扰转矩t1与由tl引起的电动机输出角位移的误差之比；

kd是伺服电动机的内阻尼系数，可直接由电动机样本查得。

三、系统参数设计

(一)系统开环增益k

通常情况下，k值在8～50s-1范围内选取，具体取值大小还应根据系统控制方式、执行元件类型、工作台质量及导轨阻尼特性等来确定。

对于点位直线控制的数控机床伺服进给系统，k值常取为8—15s-1，对于连续控制的数控机床伺服进给系统，k值常取为25s-1左右。

在闭环位置伺服系统中，通常都采用速度负反馈回路，系统的开环增益为：

在无速度反馈信号时，系统的开环增益为：

低增益伺服系统在运动时开环增益比较低，但在静止状态时，由于速度负反馈回路不起作用，因而相当于具有较高的开环增益。所以，低增益伺服系统并不影响其启动时的快速响应性和制动时的定位精度。

采用的伺服系统还常通过变开环增益的方法来改善系统性能。

在系统响应的开始阶段，采用较高的开环增益，使系统响应加快，曲线上升变陡；

在系统响应接近稳态值时，减小开环增益，使系统平稳、无超调、而且快速地趋近于稳态值。

(二)系统阻尼比ξ

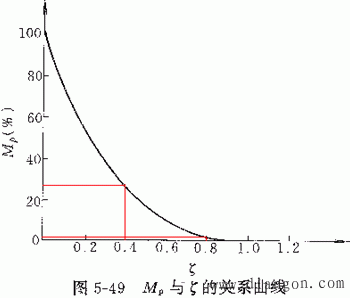
对于二阶系统，当系统允许的大超调量mp＝(25～1.5)%时，ξ可在0.4～0.8范围内选取。

影响系统阻尼比ξ的主要因素是导轨阻尼比。

增加系统阻尼比措施：

对滚动导轨预加载荷，加设阻尼器等，或通过降低系统开环增益及采用速度负反馈回路的方法来增加阻尼比。

(三)系统固有频率ωn

提高固有频率有利于改善系统稳定性和快速响应性，减小各种因素引起的误差，提高抗干扰能力，但固有频率的提高往往受系统结构、成本等条件限制。一般情况下，主要按系统稳定性要求来确定各环节的固有频率。

对于三阶系统，为保证其稳定性

若要保证系统具有大于10db的幅值稳定裕度，则要求

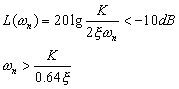
一般情况下，伺服系统中各环节的固有频率都应满足如下要求：

1)机械系统的固有频率应高于驱动系统的固有频率2～3倍

2)位置环以外的其它机械部件的固有频率应比位置环内各部件的固有频率高2～3倍。

3)如在位置环内还有速度环，则速度环的幅频交界频率应高于系统截止频率ωc，驱动系统的固有频率应高于速度环的幅频交界频率。

4)系统工作频率范围内不应包含有各环节的固有频率，以免在扰动影响下发生共振。

5)各环节的固有频率应相互错开一定距离，以免振动耦合。