西门子电抗器6SL3000-0CE21-6AA0详细说明
输出= 比例项 + 积分项 + 微分项
由于计算机从第一次采样开始每有一个偏差采样值必须计算一次输出值只需要保存偏差前值和
积分项前值利用计算机处理的重复性可以化简以上算式为
其中
Mn 在第 n 采样时刻PID 回路输出的计算值
Kc PID 回路增益
en 在第 n 采样时刻的偏差值
en – 1 在第 n-1 采样时刻的偏差值 (偏差前项)
KI 积分项的比例常数
MX 积分项前值
KD 微分项的比例常数
CPU 实际使用以上简化算式的改进形式计算 PID 输出这个改进型算式是
其中
Mn 第 n 采样时刻的计算值
MPn 第 n 采样时刻的比例项值
Min 第 n 采样时刻的积分项值
MDn 第 n 采样时刻的微分项值
比例项
比例项 MP 是增益 (Kc) 和偏差 (e) 的乘积其中 Kc 决定输出对偏差的灵敏度 偏差 (e) 是给定值
(SP) 与过程变量值 (PV) 之差CPU 执行的求比例项算式是
MPn = Kc * (SPn - PVn)
其中
MPn 第 n 采样时刻比例项的值
Kc 增益
SPn 第 n 采样时刻的给定值
PVn 第 n 采样时刻的过程变量值
= * + * + + * ( - -1 ) Mn KC en KI en MX KD en en
输出= 比例项 + 积分项 + 微分项
Mn = MPn +MIn+ MDn
输出 = 比例项 + 积分项 + 微分项
积分项
积分项值 MI 与偏差和成正比CPU 执行的求积分项算式是
MIn = Kc * TS / TI * (SPn - PVn) + MX
其中
Min 第 n 采样时刻的积分项值
Kc 增益
TS 采样时间间隔
TI 积分时间
SPn 第 n 采样时刻的给定值
PVn 第 n 采样时刻的过程变量值
MX 第 n-1 采样时刻的积分项 (积分项前值) (也称积分和或偏置)
积分和 (MX) 是所有积分项前值之和在每次计算出 MIn 之后都要用 MIn 去更新 mx 其中 MIn
可以被调整或限定 (详见“变量和范围"一节) MX 的 初值通常在第一次计算输出以前被设置为
Minitial (初值) 积分项还包括其他几个常数增益 (Kc) 采样时间间隔 (TS) 和积分时间 (TI) 其
中采样时间是重新计算输出的时间间隔而积分时间控制积分项在整个输出结果中影响的大小
微分项
微分项值 MD 与偏差的变化成正比其计算等式为
MDn = KC * TD / TS * ((SPn - PVn) - (SPn - 1 - PVn - 1))
为了避免给定值变化的微分作用而引起的跳变假定给定值不变(SPn=SPn-1) 这样可以用过程变
量的变化替代偏差的变化计算算式可改进为:
MDn = KC * TD / TS * (SPn - PVn - SPn + PVn - 1)
或
MDn = KC * TD / TS * (PVn - 1 - PVn)
其中
MDn 第 n 采样时刻的微分项值
Kc 回路增益
Ts 回路采样时间
TD 微分时间
SPn 第 n 采样时刻的给定值
SPn – 1 第 n-1 采样时刻的给定值
PVn 第 n 采样时刻的过程变量值
PVn – 1 第 n-1 采样时刻的过程变量值
为了下一次计算微分项值必须保存过程变量而不是偏差在第一采样时刻初始化为 PVn -1
PVn
回路控制类型的选择
在许多控制系统中只需要一种或二种回路控制类型例如只需要比例回路或者比例积分回路通
过设置常量参数可先选中想要的回路控制类型
如果不想要积分回路可以把积分时间设为无穷大没有积分作用积分项还是不为零因为
有初值MX
如果不想要微分回路可以把微分时间置为零
如果不想要比例回路但需要积分或积分微分回路可以把增益设为 0.0 系统会在计算积分项和
微分项时把增益当作 1.0 看待
回路输入的转换和标准化
每个 PID 回路有两个输入量给定值 (SP) 和过程变量 (PV) 给定值通常是一个固定的值比如是
设定的汽车速度过程变量是与 PID 回路输出有关可以衡量输出对控制系统作用的大小在汽车
速度控制系统中过程变量可以是测速仪的输入 (衡量车轮转速高低)
给定值和过程变量都可能是现实世界的值它们的大小范围和工程单位都可能不一样PID 指令
在对这些量进行运算以前必须把他们转换成标准的浮点型实数
转换的第一步是把 16 位整数值转成浮点型实数值下面的指令序列提供了实现这种转换的方法
XORD AC0 AC0 //清空累加器
MOVW AIW0 AC0 //把待变换的模拟量存入累加器
LDW>= AC0 0 //如果模拟量为正
JMP 0 //则直接转成实数
NOT //否则
ORD 16#FFFF0000 AC0 //先对 AC0 中值进行 符号扩展
LBL 0
DTR AC0 AC0 //把 32 位整数转成实数
转换的下一步是把实数值标准化为 0.0 1.0 之间的实数下面的算式可以用来标准化给定值
或过程变量
RNorm = (RRaw / Span) + Offset)
其中
RNorm 标准化的实数值
Rraw 没有标准化的实数值或原值
Offset 单极性为 0.0 双极性为 0.5
Span 值域大小可能*大值减去可能*小值
单极性为 32,000 (典型值)
双极性为 64,000 (典型值)
下面的指令把双极性实数标准化为 0.0 1.0 之间的实数通常用在第一步转换之后:
/R 64000.0 AC0 //累加器中的标准化值
+R 0.5 AC0 //加上偏置使其落在 0.0 1.0 之间
MOVR AC0 VD100 //标准化的值存入回路表
回路输出值转换成刻度整数值
回路输出值一般是控制变量 比如在汽车速度控制中可以是油阀开度的设置输出是
0.0 1.0 之间的标准化了的实数值在回路输出驱动模拟输出之前必须把回路输出转换成相应的
16 位整数这一过程是给定值或过程变量的标准化转换的反过程该过程的第一步把回路输出
转换成相应的实数值公式如下
RScal = (M n - Offset) * Span
其中
Rscal 回路输出的刻度实数值
Mn 回路输出的标准化实数值
Offset 单极性为 0.0 双极性为 0.5
Span 值域大小可能*大值减去可能*小值
单极性为 32,000 (典型值)
双极性为 64,000 (典型值)
这一过程可以用下面的指令序列完成
MOVR VD108,AC0 //把回路输 出值移入累加器
–R 0.5,AC0 //仅双极性有此句
*R 64000.0,AC0 //在累加器中得到刻度值
下一步是把回路输出的刻度转换成 16 位整数可通过下面的指令序列来完成
ROUND AC0 AC0 //把实数转换为 32 位整数
MOVW AC0, AQW0 //把 16 位整数写入模拟输出寄存器
正作用或反作用回路
如果增益为正那么该回路为正作用回路如果增益为负那么是反作用回路对于增益为零的积
分或微分控制来说如果积分时间微分时间为正就是正作用回路为负值则是反作
用回路
变量和范围
过程变量和给定值是 PID 运算的输入值在回路表中这些值只能被回路指令读而不能改写
输出变量是由 PID 运算产生的在每一次 PID 运算完成之后需更新回路表中的输出值输
出值被限定在 0.0 1.0 之间当 PID 指令从手动方式转变到自动方式时 回路表中的输出值可以
用来初始化输出值 (有关 PID 指令的方式详见下面的“控制方式" 一节)
如果使用积分控制积分项前值要根据 PID 运算结果更新这个更新了的值用作下一次 PID 运算
的输入当输出值超过范围 (大于 1.0 或小于 0.0) 那么积分项前值必须根据下列公式进行调整
MX = 1.0 - (MPn + MDn) 当计算输出 Mn > 1.0
[NextPage]
或
MX = - (MPn + MDn) 当计算输出 Mn < 0.0
其中
MX 经过调整了的积分和 (积分项前值)
MPn 第 n 采样时刻的比例项值
MDn 第 n 采样时刻的微分项值
Mn 第 n 采样时刻的输出值
这样调整积分前值一旦输出回到范围后可以提高系统的响应性能积分项前值也要限制在
0.0 1.0 之间在每次 PID 运算结束之后把积分项前值写入回路表 以备在下次 PID 运算
中使用
用户可以在执行 PID 指令以前修改回路表中积分项前值在实际运用中这样做的目的是找到由于
积分项前值引起的问题手工调整积分项前值时必须小心谨慎还应保证写入的值在 0.0 1.0 之
间
回路表中的给定值与过程变量的差值 ( ) 是用于 PID 运算中的差分运算用户**不要去修改此
值
控制方式
S7–200 的 PID 回路没有设置控制方式只要 PID 块有效就可以执行 PID 运算 在这种意义上
说PID 运算存在一种“自动"运行方式当 PID 运算不被执行时我们称之为“手动"方式
同计数器指令相似PID 指令有一个使能位当该使能位检测到一个信号的正跳变 (从 0 到 1) PID
指令执行一系列的动作使 PID 指令从手动方式无扰动地切换到自动方式为了达到无扰动切换
在转变到自动控制前必须用手动方式把当前输出值填入回路表中的 Mn 栏PID 指令对回路表中
的值进行下列动作以保证当使能位正跳变出现时从手动方式无扰动切换到自动方式
l 置给定值 (SPn) 过程变量 (PVn)
l 置过量变量前值 (PVn-1) 过程变量现值 (PVn)
l 置积分项前值 (MX) 输出值 (Mn)
PID 使能位的默认值是 1 在 CPU 启动或从 STOP 方式转到 RUN 方式时建立CPU 进入 RUN 方
式后使 PID 块有效没有检测到使能位的正跳变那么就没有无扰动切换的动作
报警与特殊操作
PID 指令是执行 PID 运算的简单而功能强大的指令如果其他过程需要对回路变量进行 报警等特
殊操作那么可以用 CPU 支持的基本指令实现这些特殊操作功能
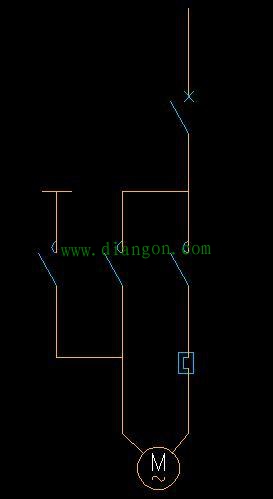
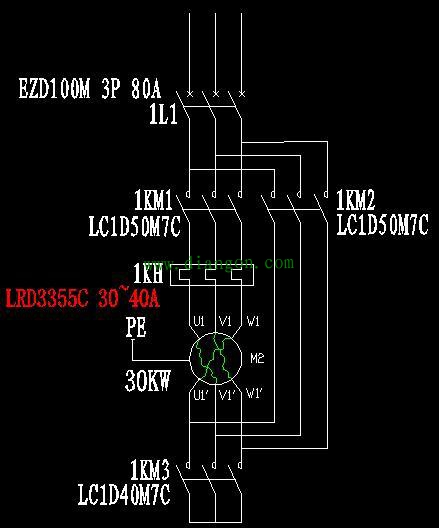
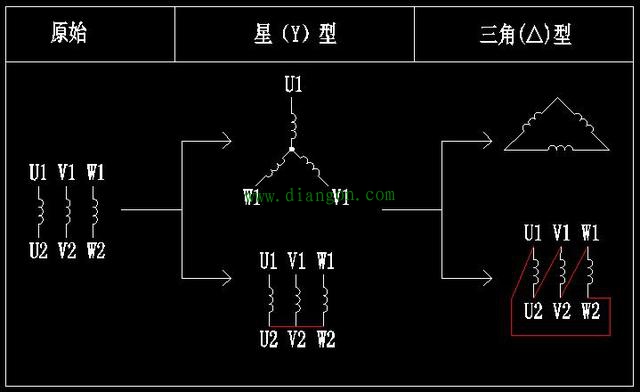
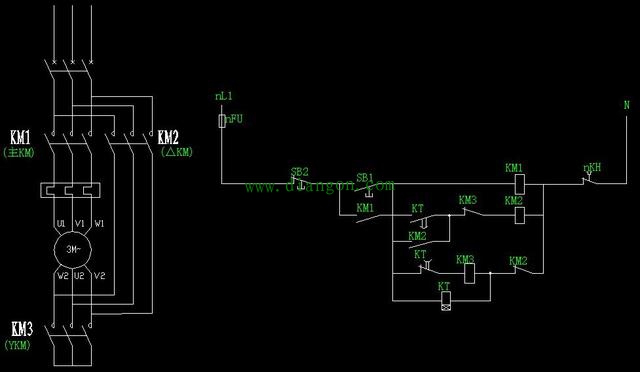
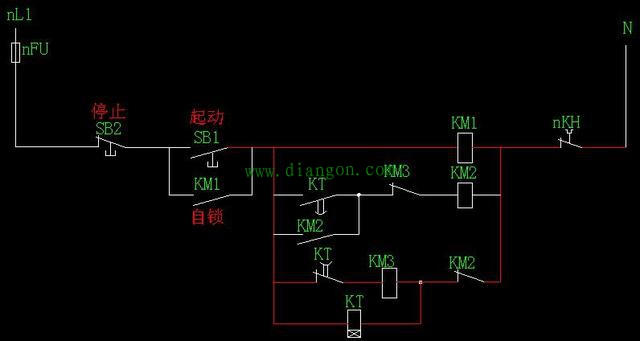
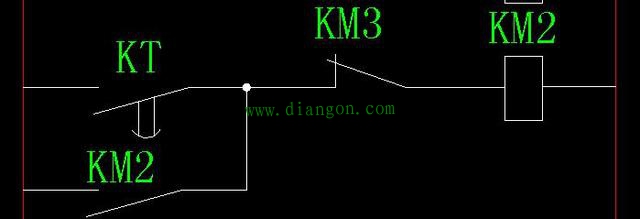
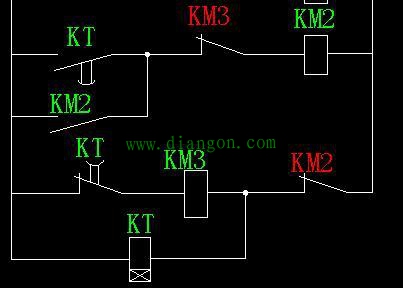
| 三相异步电动机星三角启动电气控制图详解 1.一次图画法: (1)
|